Convolutional neural network novice guide two
introduction
This article will further explore more details about convolutional neural networks. Note: Some of the contents of the following articles are more complex. In order to ensure their conciseness, some of the research documents that are explained in detail will be noted later.
Step and fill
Let's take a look back to the previous conversion layer. In the first part we mentioned filters and acceptance fields. Now we can correct the behavior of each layer by changing two main parameters. After selecting the filter size, we must also choose "step" and "fill".
Steps control how the filter convolves. In the first part we mentioned an example where the filter is convoluted around the input volume by moving one unit at a time. The total amount of filter movement is the pace. The step size is usually set in a way that the output is an integer rather than a fraction. Let's look at an example. Imagine a 7×7 input volume, a 3×3 filter (ignoring the third dimension for simplicity), and another step. This is what we are used to.
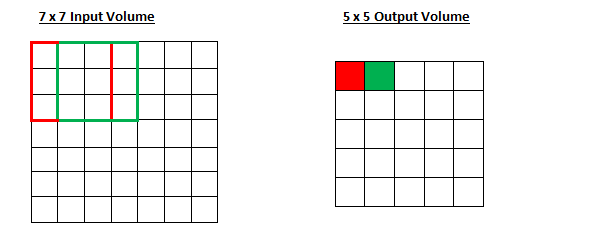
Is it the same as before? You can also try to guess what happens to the output when the stride increases to 2.
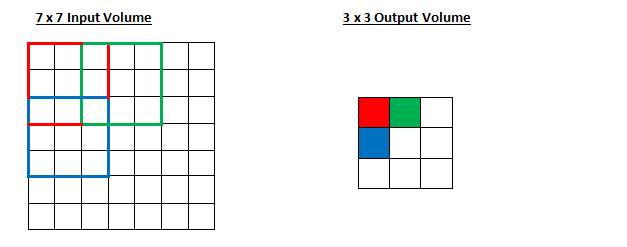
So, as you can see, the receiving field is moving in 2 units and the output will be reduced. Note that if we try to set our stride to 3, then there will be problems with both spacing and ensuring that the receiving field is suitable for the input. Usually, if programmers want to accept less field overlap and smaller space, they usually increase their stride.
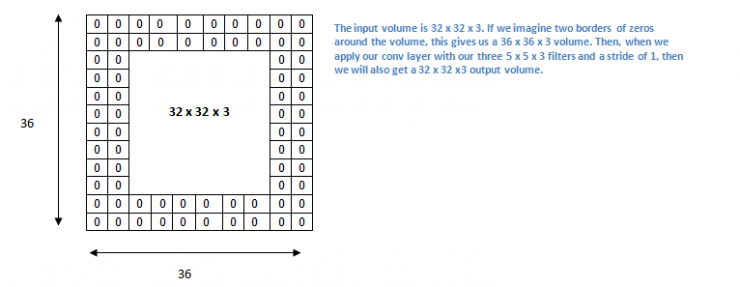
Now let's focus on padding. Before we officially begin, let's imagine a scenario. What happens when you apply three 5x5x3 filters to a 32x32x3 input volume?
Note that the space dimension decreases. As we continue to apply the convolution layer, the volume will be reduced faster than we thought. In the early layers of our neural network, we want to preserve as much raw input as possible so that we can extract these low-level features. We want to apply the same convolutional layer, but we want to keep the output at 32 x 32 x 3. To do this, we can apply a zero padding of size 2 to this layer. Zero padding fills the boundary with zero-valued input. If we consider a zero padding of size 2, then this will result in a 36×36×3 input.
If there is a step of 1 and the zero padding size is set to
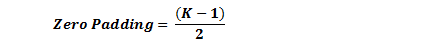
K is the size of the filter, input and output will always maintain the same spatial dimensions
The formula for the output size of any given convolutional layer

O is the output size, K is the filter size, P is the padding, and S is the step size. Â
Selecting hyperparameters
How do we determine how many layers need to be used, how many convolutional layers are there, what is the size of the filter, or the values ​​of steps and fills? These are important questions and there is no set of standards that all researchers are using. This is because neural networks largely depend on the type of data you have. The size of the data varies widely due to the complexity of the image, the type of image processing tasks, and more. When you look at your data set, one way to choose hyperparameters is to find the right combination of image abstractions in a proper range.
Modified ReLU layer
After each convolution, it is customary to add a nonlinear layer (or activation layer) immediately afterwards. The purpose of this layer is to introduce nonlinearity into the system, basically performing linear operations (only multiplication and accumulation of elements) in the convolutional layer. In the past, they were all linear algorithms such as tanh or sigmoid, but the researchers found that the ReLU layer was better because the network training speed was much faster (due to computational efficiency) and there was no significant difference in accuracy. It also helps to alleviate the problem of disappearing gradients. This is because the lower levels of network training are very slow, and gradients fall through different levels. The function used by the ReLU layer f(x) = max(0,x) input value of all values. Basically, this layer turns all negative activations to zero. This layer enhances the nonlinearity of the model and the overall network does not affect the acceptance field of the convolutional layer. Interested readers can also refer to Geoffrey Hinton's paper by Geoffrey Hinton, father of deep learning.
Pooling Layers
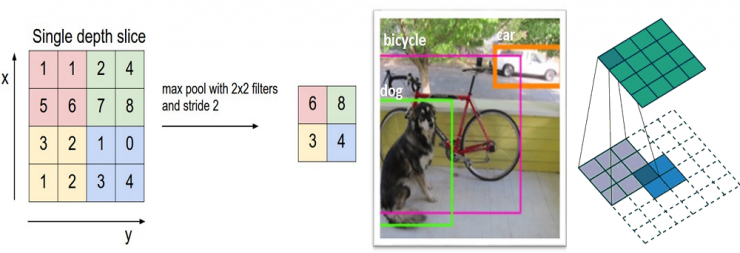
After some ReLU layers, the programmer can choose the pooling layer, which is also known as the downsampling layer. In this category, there are also several layers to choose from, but maxpooling (the largest pooling layer) is the most popular. It requires a filter (usually 2x2 in size) and an identical stride length, which is then applied at the maximum amount of input and output per partition around the filter convolution.
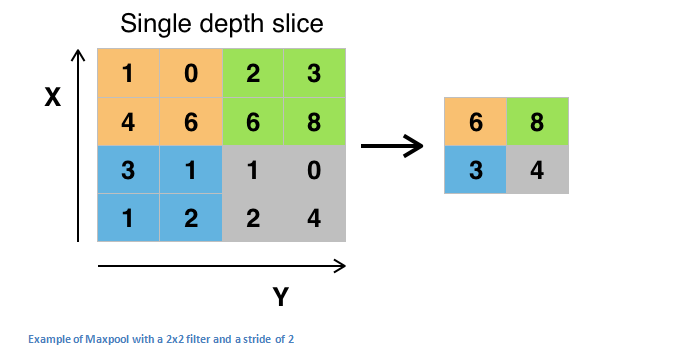
The pooling layers are also the average pooling and L2-norm pooling. The reason behind this layer is that once we know that a particular feature is its original input (which will have a high activation value), its exact location is not important. It is conceivable that this layer greatly reduces the spatial dimensions of the input volume (changes in length and width, but not depth). This has two main purposes. First, the amount of parameters or weights is reduced by 75%, which reduces computational costs. Second, it can control overfitting. This term refers to the fact that when a model is so adjusted for a training example, it cannot summarize verification and test sets. The feature of overfitting is that there is a model that can get 100% or 99% of the training set, but only 50% of the test data.
Dropout Layers
Falling down has a very special function in the neural network. In the previous section, we discussed the issue of overfitting. After training, the weight of the network is adjusted to a given training sample, so that the neural network does not perform well when given a new sample. The concept of falling layer is too simple in nature.
Dropping is to "discard" some activations randomly in this layer by setting it to zero in the forward propagation. It is as simple as this. What are the benefits of doing this in the process? To some extent, it forces the network to become "excessive." Even if some of the activations are abandoned in the process, the neural network should be able to provide correct classification or output for a specific sample. It ensures that the network will not be "appropriate" for training data, helping to alleviate over-fitting problems. The important one is used only during training and not during testing.
Network layer network
A network layer network refers to a convolutional layer that uses a 1x1 size filter. Now, at first glance you may wonder why this type of layer is helpful because the acceptance field is usually larger than their mapped space. However, we must remember that these 1x1 convolutional spans have a certain depth, so we can think of it as a 1 x 1 x N convolution, where N is the number of filter applications in that layer. This layer actually performs an ND element-level multiplication, where N is the input layer depth.
Classification, positioning, detection, segmentation
In this section we use the examples mentioned in the first section to look at image classification tasks. An image classification task is a process of recognizing and inputting an input image into a series of image classes. However, when we target the object as a task, our job is not only to obtain a classification label, but also to define the scope of an object in the image. .

There are also object detection tasks that require image positioning tasks for all objects in the image. Therefore, there will be multiple defined ranges and multiple classification labels in the image.
Finally, there is an object segmentation task. The object segmentation task refers to outputting a class label and the outline of each object in the input image.

Transfer Learning
A common misconception in deep communities today is that it is not possible to establish an effective deep learning model without the amount of data Google has. Although data is indeed an important part of creating a neural network, the concept of migration learning can help reduce the need for data. Migration learning is through a pre-trained model (the weights and parameters of the network have been trained by a large data set or others), and "fine-tuning" the process with your own data set. The idea is that the pretrained model will act as a feature extractor, removing the last layer of the network and replacing it with your own classifier (depending on your problem space). It then freezes the weights of all other layers and trains the network normally (freezing layers means that the weights can not be changed during gradient descent/optimization).
Let's find out why this would be useful, for example our pre-training model on ImageNet (ImageNet is a dataset containing 14 million images in over 1000 categories). When we consider the lower layers of the network, we know that they will detect features such as edges and curves. Now unless you have a very unique problem space and data set, your network will need to detect curves and edges. Instead of training the entire network with a randomly-initialized weight, we can use pre-trained (and frozen) model weights and focus on more important (higher) level training. If your data set is completely different from ImageNet, then you will have to train more layers and freeze some lower layers.
PS : This article was compiled by Lei Feng Network (search “Lei Feng Network†public number) and it was compiled without permission.
Via Adit Deshpande
5G Integrated Lithium Ion Battery
5G Integrated Battery,51.2V Battery System,Integrated Lithium Ion Battery,Backup Lithium Ion Battery
Wolong Electric Group Zhejiang Dengta Power Source Co.,Ltd , https://www.wldtbattery.com