Processing shadows in rasterization is not intuitive and requires a fair amount of computation: the scene needs to be rendered from the perspective of each ray, stored in the texture, and then projected again during the lighting phase. To make matters worse, doing so does not necessarily result in good image quality: those shadows are easily aliased (because the pixels considered by the light do not correspond to the pixels viewed by the camera), or are blocked (because the texels of the shadow map are stored It is a single depth value, but it can cover most of the area. In addition, most rasterizers need to support specialized shadow map "types" such as cubemap shadows (for non-directional light), or cascading shadow maps ( Used for large outdoor scenes, and this greatly increases the complexity of the renderer.
In the ray tracer, a single code path can handle all shadow scenes. More importantly, the projection process is simple and intuitive, just as light is cast from the surface to the light source and the light is checked for obstruction. The PowerVR ray tracing architecture presents a quick "temporary" ray, which is used to detect the geometry of the ray's projection direction, which also makes them particularly suitable for efficient shadow rendering.
First, first understand what is the simple process of rasterization and rasterization?Rasterization is the process of transforming geometric data into pixels after a series of transformations to render on the display device, as shown in the following figure:
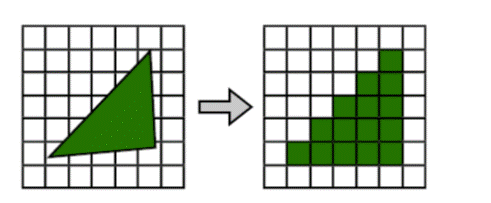
The essence of rasterization is coordinate transformation and geometric discretization, as shown below:
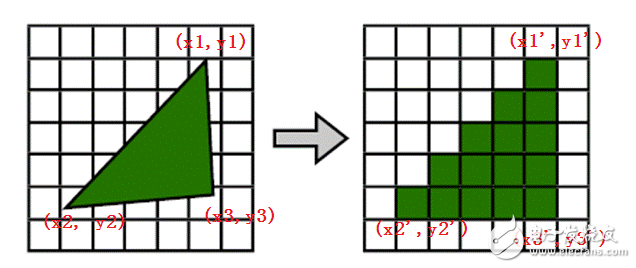
The details of the rasterization process are free to supplement.
Second, the following shows some details of texels to pixels:Upon rendering the basics of the process that Direct3D follows using rasterizing and texturing triangles, You can ensure your Direct3D application correctly renders 2D output.
When using vertices that have undergone vertex transformations as 2D output planes, we must ensure that each texel is properly mapped to each pixel region, otherwise the texture will be distorted by observing Direct3D in rasterization and texture sampling. The basic process, you can make sure your Direct3D program outputs a 2D image correctly.

Figure 1: 6 x 6 resolution display
Figure 1 shows a schematic phase pixels are modeled as squares. In reality, however, pixels are dots, not squares. Each square in Figure 1 indicates the area lit by the pixel, but a pixel is always just a dot at the center of a Square. This distinction, though seemingly small, is important. A better illustration of the same display is shown in Figure 2:
Figure 1 shows a pixel used to describe the pixel. In fact, the pixels are dots, not squares. Each square in the picture 1 shows the area lit by one pixel. However, the pixel is always a point in the middle of the square. This difference seems small but important. Picture 2 shows a better way of describing.
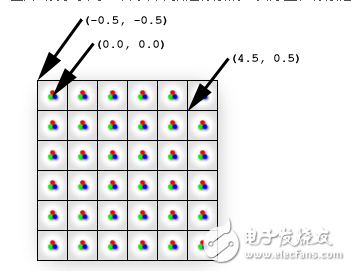
Figure 2: Display is composed of pixels
The screen space coordinate (0, 0) is located directly at the top-left pixel, and accordingly at the center of the top-left cell. The top -left corner of the display is therefore at (-0.5, -0.5) because it is 0.5 cells to the left and 0.5 cells up from the top-left pixel. Direct3D will render a quad with corners at (0, 0) and ( 4, 4) as illustrated in Figure 3.
This map correctly describes the physical pixels in the center of each cell by a single point. The origin of the screen space (0,0) is the pixel in the upper left corner, so it is in the center of the square in the top left corner. The top-left corner of the left-most upper-most square is therefore (-0.5, -0.5) because it is (-0.5, -0.5) units from the top-leftmost pixel. Direct3D will render a rectangle in the range (0,0) to (4,4), as shown in Figure 3
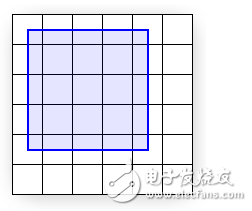
image 3
Figure 3 shows where the mathematical quad is in relation to the display, but does not show what the quad will look looks once once Direct3D rasterizes it and sends it to the display. In fact, it is impossible for a raster display to fill the quad As shown because the edges of the quad do not coincide with the boundaries between pixel cells. In other words, because each pixel can only display a single color, each pixel cell is filled with only a single color; if the display were to render the Quad exactly as shown, the pixel cells along the quad's edge would need to show two distinct colors: blue where covered by the quad and white where only the background is visible.
This process is called rasterization, and is detailed raster.
Figure 3 shows the rectangle that should be displayed mathematically. But not after Direct3D rasterization. In fact, rasterization like Figure 3 is not possible at all, because each pixel's lit area can only be one color, and it is unlikely that half of the colors will be half colorless. If it can be displayed as above, the pixel area at the edge of the rectangle must display two different colors: the blue part is represented within the rectangle, and the white part is represented outside the rectangle.
Therefore, the graphics hardware will perform the task of determining which pixels should be lit to approximate the true rectangle. This process is called rasterization. For details, see Rasterization Rules. For our particular example, the result of rasterization is shown in Figure 4.
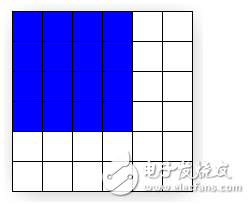
Figure 4
Note that the quad passed to Direct3D (Figure 3) has corners at (0, 0) and (4, 4), but the rasterized output (Figure 4) has corners at (-0.5,-0.5) and (3.5,3.5) . Compare Figures 3 and 4 for rendering differences. You can see that what the display actually renders is the correct size, but has been shifted by -0.5 cells in the x and y directions. However, except for multi-sampling techniques, this is the (See the Antialias Sample for thorough coverage of multi-sampling.) Be aware that if the rasterizer filled every cell the quad is the, the resulting area would be of dimension 5 x 5 instead of the desired 4 x 4 .
If you assume that screen coordinates originate at the top-left corner of the display grid instead of the top-left pixel, the quad showing exactly as expected. However, the difference becomes clear when the quad is given a texture. Figure 5 shows the 4 x 4 texture you'll map directly onto the quad.
Note that the coordinates of the two corners we pass to Direct3D (Figure 3) are (0,0) and (4,4) (relative to the physical pixel coordinates). However, the output of the rasterized output (Figure 4) has the coordinates of (-0.5, -0.5) and (3.5, 3.5). Compare the differences between Figure 3 and Figure 4. You can see that the result of Figure 4 is the correct rectangle size. However, the -0.5 pixel rectangle unit has been moved in the x and y directions. However, aside from multi-sampling techniques, this is the best way to rasterize a real-world rectangle. Note that if the pixel area of ​​all covered physical pixels is filled during rasterization, then the rectangular area will be 5x5 instead of 4x4.
If the origin of your association screen coordinate system is in the top-leftmost corner of the pixel area in the top-leftmost corner, instead of the top-leftmost physical pixel, this square is displayed as we would like it to be. However, when we give a texture, the difference becomes remarkable. Figure 5 shows a 4x4 texture used to map to our rectangle.

Figure 5
Because the texture is 4 x 4 texels and the quad is 4 x 4 pixels, you might expect the textured quad to appear exactly like the texture regardless of the location on the screen where the quad is drawn. However, this is not the case; 6 shows how a quad between (0, 0) and (4, 4) is displayed after being rasterized and textured.
Because the texture has 4x4 texels and the rectangle is 4x4 pixels, you may want to make the texture-mapped rectangle behave like a texture map. However, in fact, this is not the case. A slight change in one location point will also affect the appearance of the texture. Figure 6 illustrates how a (0,0)(4,4) rectangle is rasterized and texture mapped.
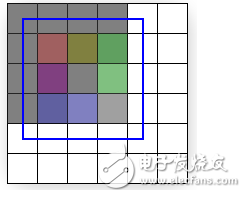
Figure 6
The quadratic in figure 6 shows the textured output (with a linear filtering mode and a clamp addressing mode) with the superimposed rasterized outline. The rest of this article explains exactly why the output looks the way it does instead of looking like the texture, But for those who want the solution, here it is: The edges of the input quad need to lie upon the boundary lines between pixel cells. By simply shifting the x and y quad coordinates by -0.5 units, texel cells will perfectly cover pixel cells And the quad can be perfectly recreated on the screen. (Figure 8 illustrates the quad at the sensitive coordinates.)
Figure 6 shows the pasted rectangle (using linear interpolation mode and CLAMP addressing mode), and the rest of the article will explain why he looks like this, unlike our texture map. First provide a solution to this problem: The border of the input rectangle needs to be between two pixel areas. By simply shifting the x and y values ​​by -0.5 pixel area units, the texels will perfectly cover the rectangular area and be reproduced on the screen (Figure 8 illustrates the correct coordinates of this perfect overlay). Translator: The coordinates of the window you create must be integers, so in the center of the pixel area, the boundary of the left-most pixel area of ​​your client area screen must be in the center of a certain pixel area before shifting -0.5.)
The details of why the rasterized output only bears slightly resemblance to the input texture are initially related to the way Direct3D addresses and samples textures. Whats assume assumes you have a good understanding oftexture coordinate space And bilinear texture filtering.
There are only a few reasons why rasterized and texture-mapped images are related to our original texture maps and Direct3D texture addressing modes and filtering modes.
The back to our investigation of the strange pixel output, it makes sense to trace the output color back to the pixel shader: The pixel shader is called for each pixel selected to be part of the rasterized shape. The solid blue quadgs in FIG. 3 Could have a particularly simple shader:
Returning to our investigation of why strange pixels are output, in order to track the color of the output, we look at the pixel shader: Each pixel in the pixel behind the raster is called once. The rectangular area around the blue wireframe in Figure 3 uses a simple color filter:
Float4 SolidBluePS() : COLOR
{
Return float4( 0, 0, 1, 1 );
}
For the textured quad, the pixel shader has to be changed slightly:
Texture MyTexture;
Sampler MySampler =
Sampler_state
{
Texture = "MyTexture";
MinFilter = Linear;
MagFilter = Linear;
AddressU = Clamp;
AddressV = Clamp;
};
Float4 TextureLookupPS( float2 vTexCoord : TEXCOORD0 ) : COLOR
{
Return tex2D( MySampler, vTexCoord );
}
That code assumes the 4 x 4 texture of Figure 5. The pixel shader gets called once for each rasterized pixel, and each time the returned color is The sampled texture color at vTexCoord. Each time the pixel shader is called, the vTexCoord argument is set to the texture coordinates at that pixel. That means the shader is asking the texture sampler for the filtered texture color at the exact location of the pixel, As detailed in Figure 7:
The code assumes that the 4x4 texture in Figure 5 is stored in MyTexture. MySampler is set to bilinear filtering. This Shader is called once for each pixel when rasterizing. Each returned color value is the result of a sampled texture using vTexCoord, which is the texture coordinate at the physical pixel value. This means that the texture is queried for the position of each pixel to get the color value of this point. Details are shown in Figure 7:
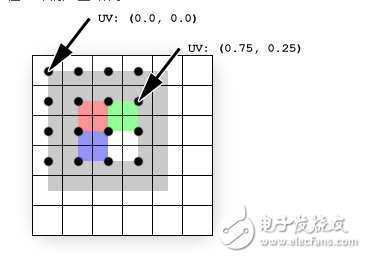
Figure 7
The texture (shown superimposed) is sampled directly at pixel locations (shown as black dots). Texture coordinates are not affected by rasterization (they remain in the projected screen-space of the original quad). The black spots show where the rasterization pixels are. The texture coordinates at each pixel are easily determined by interpolating the coordinates stored at each vertex: The pixel at (0,0) coincides with the vertex at (0, 0); therefore, the Texture coordinates at that pixel are simply the texture coordinates stored at that vertex, UV (0.0, 0.0). For the pixel at (3, 1), the interpolated coordinates are UV (0.75, 0.25) because that pixel is located at three-fourths of the texture's width and one-fourth of its height. These interpolated coordinates are what get passed to the Pixel shader.
The texture (overlapped area) is sampled at the location of the physical pixel (black dot). Texture coordinates are not affected by rasterization (they are retained in the original coordinates projected into the screen space). Black points are the locations of rasterized physical pixels. The texture coordinate value of each pixel can be obtained by simple linear interpolation: the vertex (0,0) is the physical pixel (0,0) and the UV is (0.0,0.0). The pixel (3,1) texture coordinate is UV (0.75, 0.25) because the pixel value is at the 3/4 texture width and 1/4 texture height. These interpolated texture coordinates are passed to the pixel shader.
The texels do not line up with the pixels in this example; each pixel (and therefore each sampling point) is positioned at the corner of four texels. Because the filtering mode is set to Linear, the sampler will average the colors of the four texels Sharing that corner. This explains why the pixel expected to be red is actually three-fourths gray plus one-fourth red, the pixel expected to be green is one-half gray plus one-fourth red plus one-fourth green, and so on .
Each texel does not overlap each pixel, and each pixel is in the middle of four texels. Because the filter mode is bilinear. The filter will take the average of 4 colors around the pixel. This explains why the red we want is actually 3/4 gray plus 1/4 red. The pixels that should be green are 1/2 gray plus 1/4 red plus 1/4 green.
To fix this problem, all you need to do is correctly map the quad to the pixels to which it will be rasterized, and visitors map the texels to pixels. Figure 8 shows the results of drawing the same quad between (-0.5, - 0.5) and (3.5, 3.5), which is the quad intended from the outset.
In order to fix this problem, all you need to do is map the rectangle to the pixels correctly, and then correctly map the texels to the pixels. Figure 8 shows the result of texture mapping of (-0.5, -0.5) and (3.5, 3.5) rectangles.
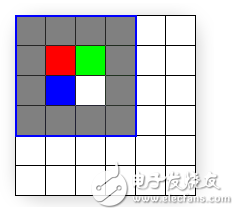
Figure 8
Summary
In summary, pixels and texels are actually points, not solid blocks. Screen space originates at the top-left pixel, but texture coordinates originate at the top-left corner of the texture's grid. Most importantly, remember to subtract 0.5 units from the x And y components of your vertex positions when working in the screen space space in order to correctly align texels with pixels.
to sum up:In general, pixels and texels are actually points, not solid blocks. The screen space origin is the physical pixel in the upper left corner, but the texture coordinate origin is the top left corner of the texel rectangle. Most importantly, remember that when you want to correctly map the texels in the texture to the pixels in the screen space, you need to subtract 0.5 units.
Draw-wire sensors of the wire sensor series measure with high linearity across the entire measuring range and are used for distance and position measurements of 100mm up to 20,000mm. Draw-wire sensors from LANDER are ideal for integration and subsequent assembly in serial OEM applications, e.g., in medical devices, lifts, conveyors and automotive engineering.
Linear Encoder,Digital Linear Encoder,Draw Wire Sensor,1500Mm Linear Encoder
Jilin Lander Intelligent Technology Co., Ltd , https://www.jllandertech.com