Use external LNA to improve receiver sensitivity
Abstract: This application note discusses the impact of adding a low-noise amplifier (LNA) to the system specifications in a remote control gating (RKE) receiver. The system sensitivity will increase by 3.77dB, but the third-order intercept point will decrease by 15dB.
The sensitivity index represents the receiver's ability to capture weak signals. Since this index directly affects the communication range of the system, it is critical for system design.
In many remote control gating (RKE) and tire pressure monitoring (TPM) designs, manufacturers generally use receiver sensitivity (dBm) as a key different from their competitors. In addition, other receiver parameters such as noise figure, intermodulation distortion, dynamic range, and even power consumption are also important parameters because consumers value the sensitivity and communication range.
One way to improve system sensitivity is to connect an external LNA to increase the link gain. Perhaps there are other simple methods?
Receiver sensitivity depends on the noise figure of the system, the minimum S / N ratio required for demodulation detection, and the thermal noise of the system. The minimum input signal level is as follows:
| S = NF + n0 + S / N | EQN1 |
In the formula, S is the required minimum input signal (dBm), NF is the receiver noise figure, S / N is the output signal-to-noise ratio (can correctly detect the signal, usually corresponding to the acceptable bit error rate), n0 is the receiver The thermal noise power of the machine (dBm).
To simplify the calculation, it is estimated that the output S / N (Manchester data) is required to be 5dB. In order to get S, you also need to know n0, which is defined as:
| n0 = 10log10 (k TB / 1E-3), the unit is dBm |
In the formula, k is the Boltzmann constant (1.38 E-23), T is the Kelvin temperature, and B is the system noise bandwidth. At room temperature (T = 290 ° K), for a 1Hz bandwidth, n0 = -174dBm (usually expressed as equal to -174dBm / Hz).
For a 300kHz IF bandwidth, n0 is -119dBm.
Assume that the system sensitivity is -109dBm. With EQN1, the NF of the receiver can be determined to be 5dB. According to the relationship between noise factor (NF) and noise factor (F):
| (NF) db = 10logF and F = 10 (NFdb / 10) |
The noise factor is: F = 3.162.
The following equation can be used to calculate the cascade noise factor of multiple two-port devices:
| FTotal = F1 + (F2-1) / G1 + (F3-1) / (G1 × G2) + ... | EQN2 |
If an external LNA is added to the input of our system, we can use EQN2 to calculate the new noise factor. For the MAX2640 LNA, NF = 1dB (F1 = 1.26) and gain is 15dB (G1 = 31.62). Since the noise factor of the original system (MAX1470) is F2 = 3.162, then the resulting FTotal = 1.327 or 1.23dB.
What is the final impact on the system indicators? Using EQN1, we can get the current sensitivity as:
| S = 1.23-119 + 5 = -112.77db |
Therefore, the addition of an external LNA can increase the system sensitivity by 3.77dB, depending on the specific situation. After all, the noise figure is only a part of the system index. The MAX1470 has a system IIP3 of -34dBm. This parameter is based on an internal mixer IIP3 of -18dBm and an internal LNA gain of 16dB, resulting in an IIP3 of -34dBm. After adding an external MAX2640 LNA, the system's IIP3 is reduced from -34dBm to -49dBm (LNA gain is 15dB), which means that the system's signal processing capability is reduced. In other words, although the system sensitivity is increased by nearly 4dB, the dynamic range of the system is reduced by 15dB.
Therefore, system designers need to judge whether it is worth reducing IIP3 in order to improve system sensitivity.
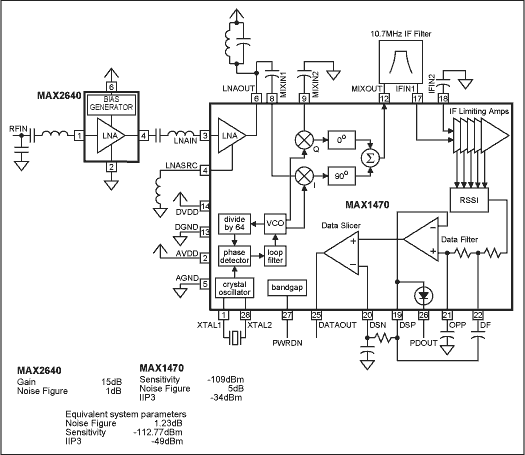
figure 1.
Security Siren,Keyboard Siren,Keyboard Play Siren,Keyboard Play Alarm
NINGBO SANCO ELECTRONICS CO., LTD. , https://www.sancobuzzer.com