One-dimensional and three-dimensional convolution processes and their applications in machine vision

Due to the explosion of computer vision, the use of two-dimensional convolution is the most widely used. Therefore, this paper first introduces two-dimensional convolution, and then introduces the specific flow of one-dimensional convolution and three-dimensional convolution, and describes their specific applications.

1, two-dimensional convolution

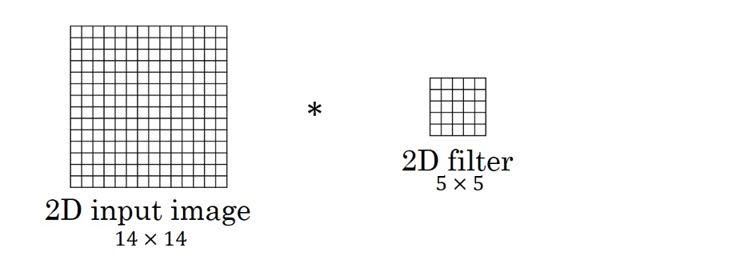
• The input data dimension in the graph is 14 × 14 and the filter size is 5 × 5, the two are convolved, and the output data dimension is 10 × 10 (14 − 5 + 1 = 10).

• The above content does not introduce the concept of a channel. It can also be said that the number of channels is 1. If the number of channels input in the two-dimensional convolution is changed to three, the input data dimension becomes (14 × 14 × 3). Since the number of channels of the filter in the convolution operation must be the same as the number of channels of the input data, the filter size also becomes 5 × 5 × 3 . In the convolution process, the filter and data are convolved in the channel direction, and then the convoluted values ​​are added. That is, 10 × 10 operations of adding 3 values ​​are performed. The final output data dimension is 10 × 10.

• The above discussion is based on a filter number of one. If you increase the number of filters to 16, that is, 16 filters of size 10 × 10 × 3, the final output data dimension becomes 10 × 10 × 16. It can be understood that the convolution operation of each filter is performed separately, and the output of each convolution is finally concatenated in the third dimension (channel dimension).

• Two-dimensional convolution is commonly used in computer vision and image processing.

2, one-dimensional convolution

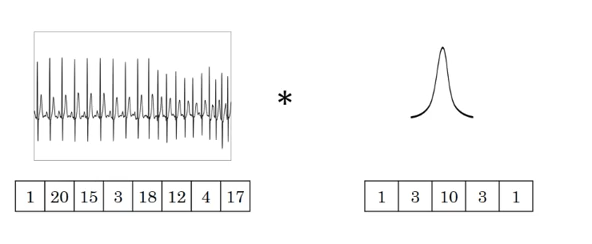
• The input data dimension in the graph is 8 and the filter dimension is 5. Similar to two-dimensional convolution, the data dimension output after convolution is 8−5+1=48−5+1=4.

• If the number of filters is still 1, the number of channels of the input data becomes 16, that is, the input data dimension is 8 × 16 . The concept of the channel here is equivalent to embedding in natural language processing, and the input data represents 8 words, where the word vector dimension of each word is 16 in size. In this case, the dimension of the filter changes from 5 to 5 × 16 and the final output data dimension is still 4.

• If the number of filters is n, the output data dimension becomes 4 × n.

• One-dimensional convolution is often used in sequence models, in the field of natural language processing.

3, three-dimensional convolution

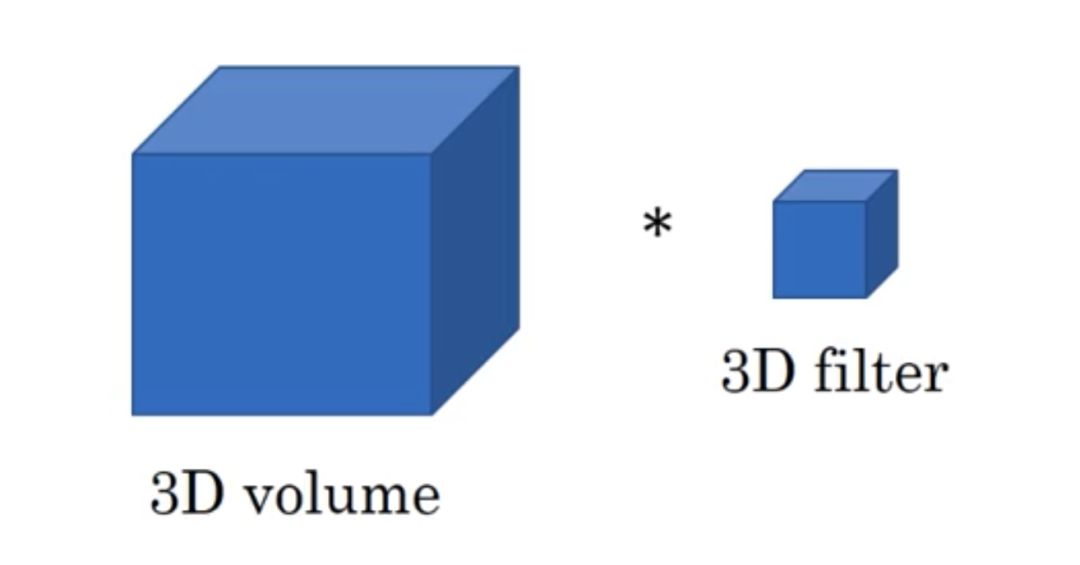
Here, algebraic methods are used to introduce three-dimensional convolutions. The specific idea is the same as one-dimensional convolution or two-dimensional convolution.

• Assume that the input data size is a1 × a2 × a3, the number of channels is c, and the filter size is f, that is, the filter dimension is f × f × f × c (the dimensions of the channel are not normally written), and the number of filters is n. .

• Based on the above, the final output of three-dimensional convolution is (a1 − f + 1) × (a2 − f + 1) × (a3 − f + 1) × n. The formula is still valid for one-dimensional convolutions, two-dimensional convolutions, and only removes incoherent input data dimensions.

• Three-dimensional convolution is commonly used in the medical field (CT influence), video processing field (detection action and character behavior).